数据结构¶

算法可视化具体实现方式可能有出入

王道计算机考研数据结构_哔哩哔哩_bilibili

1 绪论¶

1.1 数据结构基本概念¶

数据结构三要素：

逻辑结构
物理结构
数据的运算

数据逻辑结构：

集合
线性
树形
图

数据存储结构：

顺序存储
链式存储
索引存储
散列存储（哈希存储）

1.2 算法的基本概念¶

算法五个特性：

有穷性
确定性
可行性
输入
输出

好算法的特质：

正确性
可读性
健壮性
高效率和低存储

时间复杂度：常对幂指阶

$O(n^3)<O(2^n)<O(n!)<O(n^n)$

空间复杂度：空间复杂度是指算法需要的辅助空间的复杂度

递归时的空间复杂度，$O(mn)$ ，$O(m)$ 是每次递归中定义的变量的空间复杂度，$O(n)$ 是递归深度复杂度

2 线性表¶

2.1 线性表的基本概念和基本操作¶

线性表的基本操作：创销，增删改查

2.2 顺序表¶

顺序存储的线性表

实现方式：静态分配，动态分配

2.3 链表¶

单链表：带头结点和不带头结点
不带头结点时，对第一位结点操作有时要特殊处理
指定结点的前插操作（给一个结点和要插入的数据），可以在结点后面插入然后交换两者的数据
指定结点的删除操作，得到后继结点的数据并删除后继结点
头插可以用于链表的逆置
双链表
循环链表
循环单链表
循环双链表
静态链表

3 栈和队列¶

3.1 栈¶

LIFO

栈的实现：

顺序实现
初始化 top = -1
初始化 top = 0
共享栈
链式实现，用单链表实现，头插，头删

卡特兰数： $$ \frac{1}{n+1}C^n_{2n} $$

3.2 队列¶

FIFO

队列的实现:

顺序实现
设置队首和队尾指针，队尾指向队尾元素的下一个
判断为空， rear == front
判断队列空或满
- (rear + 1) % size == front（循环队列），留一个位置的原因是为了不和判断为空冲突
- 定义队列长度的变量，定义的话队列可以多一个空间，且一个 int 占用的空间很可能比存储的队列元素小
- 定义 tag 表示上一次操作是插入还是删除，0 表示删除，1 表示插入；tag 初始化为 0（只有插入才可能导致队空）
队列元素个数：(rear + size - front) % size
链式实现
定义头指针和尾指针
尾插首删

双端队列：

队首和队尾都可以插入和删除
输入受限的双端队列：一端插入，双端输出
输出受限的双端队列，一端输出，双端输出

3.3 栈和队列的应用¶

栈的应用：

括号匹配
表达式求值
波兰表达式（前缀表达式），逆波兰表达式（后缀表达式）；
计算后缀表达式时栈中存放操作数，从左往右扫描后缀表达式；
计算前缀表达式时存放操作数，从右往左扫描前缀表达式，需要注意除法和减法时操作数运算的顺序和后缀表达式不一样；
中缀表达式转换后缀表达式时栈中存放运算符和括号，弹出优先级大于或等于要压栈的运算符，遇到右括号就都弹出直到遇到左括号
中缀表达式的计算：中缀转后缀，计算后缀；要用到 2 个栈一起操作
递归，函数调用时在栈中压入下一条指令的地址和函数中需要的变量

队列的应用：

树的层次遍历
图的bfs
操作系统分配系统资源，FCFS，first come first server

3.4 特殊矩阵压缩存储¶

二维数组的行优先和列优先

对称矩阵：只存储对角线和上或下三角区，然后用行优先或者列优先存储

三角矩阵：和对称矩阵类似，上三角矩阵多存储一个下三角中的常数，下三角类似

三对角矩阵（带状矩阵）：只存储 $|i-j| <= 1$ 的元素，除了第一行和最后一行每行都有三个元素

稀疏矩阵：三元组，十字链表

4 串¶

4.1 串的存储结构¶

顺序存储
链式存储

4.2 串的模式匹配¶

主串，子串，模式串

朴素的匹配算法复杂度：$O(mn)$

KMP：字符串下标从 0 开始

// 字符串下标从 0 开始
// next
void getNext(char *p, int *next) {
    next[0] = -1;
    int i = 0, j = -1;
    while(i < strlen(p))
        if(j == -1 || p[i] == p[j]){
            i++, j++;
            next[i] = j;
        }
        else j = next[j];
}
// KMP
// 主体字符串 匹配字符串
int KMP(char *s, char *p){
    int i = 0;
    int j = 0;
    while(i < strlen(s) && j < strlen(p))
        if(j == -1 || s[i] == p[j]) i++, j++;
        else j = next[j];
    // 返回存在与 p 相同的字串的位置
    if(j == strlen(p)) return i-j;
    else return -1;
}

KMP 优化：nextval 数组

5 树¶

要注意不要把树的性质，二叉树的性质，完全二叉树的性质搞混，当然，二叉树也有树的性质，完全二叉树也有二叉树的性质

5.1 树的基础知识和性质¶

基础知识：

树的概念
祖先节点，子孙结点，父节点，孩子结点，兄弟结点，堂兄弟结点
路径（从上到下,兄弟结点之间不存在路径），路径长度，树的路径长度（根到所有结点路径长度之和）
结点的层次（深度），度，树的高度（深度），树的度（各结点的度的最大值）
有序树（不可以交换），无序树
森林

树的性质

结点数 = 总度数 + 1
度为 m 的树和 m 叉树的区别，m 叉树的度不一定为 m
度为 m 的树第 i 层至多有 $m^{i-1}$ 各结点
高度为 h 的 m 叉树至多有 $\frac{m^h-1}{m-1}$
高度为 h 的 m 叉树至少有 h 个结点，高度为 h，度为 m 的树至少有 h+m-1 个结点
n 个结点的 m 叉树的最小高度 $ceil(\ \ log_m(n(m-1)+1)\ \ )$

5.2 二叉树¶

二叉树特点：

每个节点至多只有两棵子树
二叉树是有序树

特殊的二叉树:

满二叉树，不存在度为 1 的结点
完全二叉树，至多只有一个度为 1 的结点，只有一个孩子的结点一定是有左孩子
二叉排序树
平衡二叉树，不要求是二叉排序树

二叉树性质：

树的性质
$n=n_0+n_1+n_2,n=2n_2+n_1+1$ 得到 $n_0 = n_2 + 1$

完全二叉树性质：

高度 $h=ceil(\ log_2(n+1)\ ) 或 floor(\ log_2n\ )+1$
$n_1=0或1$
$n_0=n_2+1$ 得 $n_0+n_2$ 一定是奇数
若完全二叉树有 2k 个结点，则 $n_1=1,n_0=k,n_2=k-1$，若完全二叉树有 2k-1 个结点，则 $n_1=0,n_0=k,n_2=k-1$

二叉树的存储结构

顺序存储
链式存储
n个结点有 2n 个指针，n-1 个没有指向 NULL，所以有 n+1 个指向 NULL
二叉链表，三叉链表（带父结点）

5.3 二叉树的遍历¶

层次遍历：队列

先序遍历：前缀表达式

中序遍历中：中缀表达式（无括号）

后序遍历：后缀表达式

非递归的代码实现方式：利用栈；后续遍历的非递归比较难

由遍历序列构造二叉树

前序+中序
后序+中序
层序+中序

5.4 线索二叉树¶

二叉树的线索化和线索二叉树的遍历的代码

增加 2 个标志位表示左右孩子指针是否是线索，注意在线索二叉树遍历时遍历左右子树时要判断是否是前后继（如果不判断，在前序遍历时会绕圈）

中序线索二叉树

先序线索二叉树

后序线索二叉树

中序前驱，中序后继

前序前驱，前序后继

后序前驱，后序后继

二叉树的线索化：

前序线索化时要注意判断 tag；
函数体主要由 2 个线索化左右子树的递归调用组成，还有利用参数的 pre 建立 pre 的后继和当前结点的前驱；不同的遍历方式顺序不同

线索二叉树中找前序和后继：

中序
先序：找前驱结点如果没有父节点找不到，如果有父节点需要分四种情况（第四种根结点）
后序：找后继序也需要三叉链表，分四种情况（第四种根结点）

5.5 树的存储结构和遍历¶

存储结构：

双亲表示法（顺序存储），增加结点，删除结点
孩子表示法（顺序+链式）
孩子兄弟表示法（链式存储），两个指针：第一个孩子和右兄弟指针（树和二叉树的转换，森林和二叉树的转换）

树的遍历：

先根遍历（和转换为二叉树后的先序遍历一样）
后根遍历（和转换为二叉树后的中序遍历一样）
层次遍历（队列，bfs）

森林的遍历：

先序遍历，依序对子树进行先序遍历（和转换为二叉树后的先序遍历一样）
中序遍历，依序对子树进行后根遍历（和转换为二叉树后的中序遍历一样）

5.6 二叉排序树，平衡二叉树，哈夫曼树¶

二叉排序树（BST）：

构造，查找，增加
删除：要删除的结点时叶子节点，只有左子树，只有右子树，左右子树都有（把右子树最小的数或者左子树最大的数搬上来，即中序遍历中的直接前驱和直接后继）
平均查找长度（ASL），查找失败的ASL

平衡二叉树（AVL，发明人首字母组成或者 BBT）：二叉排序树的特殊形式，左子树和右子树的高度差不超过 1

平衡因子，结点的平衡因子=左子树高-右子树高，AVL 中所有结点的平衡因子只有 -1，0，1
最小不平衡子树
调整最小不平衡子树
LL，右旋
RR，左旋
LR，先左旋，再右旋
RL，先右旋，再左旋
查找效率分析：$O(log_2n)$ :

假设 $n_h$ 表示高度为 $h$ 的平衡二叉树的的最少结点数，有 $n_0=0, n_1=1, n_2=2, n_h=n_{h-1}+n_{h-2}+1$

哈夫曼树（是二叉树）：

结点的权，结点的带权路径长度：根到结点的路径长度 x 结点权值，树的带权路径长度（WPL）：树中所有叶子结点的带权路径长度之和
哈夫曼树：WPL最小的二叉树，也称最优二叉树
哈夫曼树的构造：先选 2 个权值最小的结点加起来变成一个新的结点 .....
哈夫曼树的总结点树为 $2n-1$，n 个叶子结点，多出来 n-1 个新结点；哈夫曼树不存在度为 1 的结点；哈夫曼树并不唯一，但 WPL 一定最优
哈夫曼编码，非前缀编码会有歧义

5.7 红黑树¶

红黑树是满足以下红黑性质的二叉排序树（不是二叉平衡树）：

每个结点是红色或者黑色的
根结点是黑色的
叶结点（虚构结点，NULL）都是黑色的
不存在相邻的红结点
对每个结点，从该结点到任一叶结点的简单路径上的黑结点的数量相同（黑高）；根的黑高是红黑树的黑高

结论1：

从根到叶结点的最长路径不大于最短路径的2倍
从根到任一叶结点的简单路径最短时，这条路径必然全是黑结点
当某条路径最长时，这条路径是由黑结点和红结点相间构成的，红结点和黑结点的数量相同

结论2：

有n个内部结点的红黑树的高度 $h<=2log_2(n+1)$ ；证：根的黑高至少为 h/2，于是有 $n>=2^{h/2}-1$ 即可

综上：红黑树是适度平衡的，由AVL的高度平衡变成了任一结点的左右子树的高度不相差2倍

红黑树的插入结点$z$：

用二叉查找树插入法插入，并把 $z$ 涂成红色，如果 $z$ 父结点是黑色的，无需做调整
如果 $z$ 是根结点，涂黑然后树的黑高加一
如果 $z$ 不是根结点，并且 $z.p$ 是红色的（$z.p.p$ 是黑色的），分为以下三种情况：
- 情况一：$z$ 的叔结点 $y$ 是黑色的，且 $z$ 是右孩子；解决办法：先左旋（变成了情况二），再右旋
- 情况二：$z$ 的叔结点 $y$ 是黑色的，且 $z$ 是左孩子；解决办法：右旋，$z.p$ 和 $z.p.p$ 要互换颜色
- 如果 $z.p$ 是 $z.p.p$ 的右孩子，则和上面的两种情况是对称的
- 情况三：如果 $z$ 的叔结点 $y$ 是红色的；不管 $z$ 是左孩子还是右孩子，把爷结点变成红色，把父结点和叔结点变成黑色，然后爷结点变成新的 $z$ 继续处理，即 $z$ 上移了两层

红黑树的删除：可以参考的blog

用二叉查找树的删除结点的办法
第1种情况：如果被删除结点有左右孩子，就把其中序遍历的后继（或者前驱）结点的数值与其替换，问题变换成下面2中情况
第2种情况：待删结点只有左孩子或者右孩子，那么只有可能待删除的是黑色，左孩子或者右孩子是一个红色结点，把结点删了然后把孩子换上来变成黑色即可
第3种情况：待删结点没有孩子
- 待删结点没有孩子并且是红色的，直接删除即可
- 待删结点是黑色的，删除待删结点后变成 null 结点再套一层黑色（或者是双黑结点）代替，叫做 $x$，问题变为如何把多的那层黑色消去，区别在于 $x$ 的兄弟结点 $w$ 以及 $w$ 的孩子结点的颜色
  - 情况1：$w$ 是红色的，那么 $w$ 必然是有黑色左右孩子，处理办法是交换 $x.p$ 和 $w$ 的颜色，既然后进行一次单向旋转，问题变为情况2，3 或 4
  - 情况2：$w$ 是黑色的，$w$ 的左孩子是红色的，$w$ 的右孩子是黑色的；即红色结点是爷结点的右孩子的左孩子，处理办法是先交换 $w$ 和其左孩子的颜色再 RL，其中右旋过后其实就变成了情况3
  - 情况3：$w$ 是黑色的，$w$ 的右孩子是红色的；处理办法是先交换 $w$ 和 $x.p$ 的颜色，再把 $w$ 右孩子变为黑色再 RR(左单旋)，然后 $x$ 可以变回正常黑色
  - 情况4：$w$ 是黑色的且两个孩子结点也都是黑色（或者说无红色子结点）的处理办法是把 $w$ 和 $x$ 去掉一层黑色，给 $x.p$ 加上一层黑色作为新的 $x$ 去处理（如果 $x.p$ 是红色的就直接涂黑，如果是黑色的就作为双黑结点继续处理）；如果一直处理到根结点，把多的一层黑色直接舍去
  - 其他对称情况类似

6 图¶

6.1 图的基本概念¶

线性表可以是空表，树可以是空树，图不可以是空，即 V 一定是非空集，E 可以为空集

无向图，有向图：顶点的有序和无序；弧（有向边）

简单图：无重边，无环；多重图：非简单图

完全图：也称简单完全图，有向与无向

子图：从 V 中取子集，E 做相应的子集；生成子图：$V(G')=V(G)$

连通：无向图中 v 和 w有路径存在；强连通：无向图中 v 和 w有路径存在，w 到 v 有路径存在

连通图（无向图），n 个点最少有 n-1 条边，最多有 $C_{n-1}^2$ 即（$\frac{(n-1)(n-2)}{2}$）条边，n-1个顶点构成完全图

强连通图（有向图），n 个点最少有 n 条边

连通分量：无向图中的极大连通子图称为连通分量

强连通分量：有向图中的极大强连通子图称为连通分量

生成树：连通图中，包含连通图的全部顶点，且是极小连通子图；少一条边就非连通，多就有环

生成森林：非连通图中，连通分量的生成树构成了生成森林

邻接，关联：无向图中 $(v, v')$，$v,v'$ 互为邻接点，$(v, v')$ 和 $v,v'$ 相关联；有向图中 $<v, v'>$，称 $v$ 邻接到 $v'$，$<v, v'>$ 和 $v,v'$ 相关联

度（TD），出度（OD），入度（ID）；有向图的度为入度 + 出度

无向图：$\sum TD(V_i)=2|E|$

有向图：$\sum OD(V_i)=\sum ID(V_i)=|E|$

边的权，带权图（也叫网），带权路径长度

路径：顶点序列

回路

简单路径：顶点不重复出现；简单回路：除了起点和终点，顶点不重复

距离：最短路径长度或无穷

稀疏图，稠密图

树：不存在回路且连通的图；森林：

有向树：只有一个顶点的入度为0，其他顶点的入度都为 1

6.2 图的表示法和基本操作¶

邻接矩阵法（空间复杂度 $O(v^2)$），假设矩阵为 $A$，则 $A*A$ 表示路径长度为 2 的路径数目，$A^n$ 表示路径长度为 n

邻接表（空间复杂度有向图 $O(V+E)$，无向图 $O(V+2E)$）

十字链表（存储有向图，空间复杂度 $O(V+E)$）

邻接多重表（存储无向图，空间复杂度 $O(V+E)$）

6.3 bfs && dfs¶

bfs：队列，空间复杂度 $O(V)$ （队列的长度）时间复杂度邻接矩阵 $O(V^2)$，邻接表 $O(V+E)$

广度优先生成树（不是最小的，且如果用邻接表不唯一）

广度优先生成森林（图中有多个连通分量时）

dfs：空间复杂度 $O(V)$（函数递归调用栈）时间复杂度邻接矩阵 $O(V^2)$，邻接表 $O(V+E)$

深度优先生成树（不是最小的，且如果用邻接表不唯一）

深度优先生成森林（图中有多个连通分量时）

判环用拓扑排序和 dfs，如果在 dfs 要访问的元素已经访问过并且还在栈中时，说明有环；bfs 不行的原因是可能有多个结点指向该结点，不一定是因为有环

6.4 最小生成树和最短路¶

最小生成树（MST），非连通图只有生成森林

Prim：$O(V^2)$
Kruskal（并查集）：$O(ElogE)$

最短路径

各顶点间最短路
Floyd（带权图，无权图），可以用 path 记录中转点来记录路径，时间复杂度 $O(V^3)$，空间复杂度 $O(V^2)$
单源最短路问题
BFS（无权图）
Dijkstra（带权图，无权图），注意与 Prime 算法的区别在 dis 的含义和松弛操作；记录每个结点的前驱来记录路径，时间复杂度 $O(V^2)$。不适用于负权边

6.5 有向无环图与应用¶

有向无环图（DAG，Directed acyclic graph）

描述表达式，并进行图的优化
AOV 网（Activity On Vertex NetWork），用 vertex 表示活动
拓扑排序：
算法：入度的统计可以用一个数组indegree实现，E是删除结点时更新indegree需要的时间，用队列或栈记录indegree为0的结点
时间复杂度，邻接表 $O(V+E)$，邻接矩阵 $O(V^2)$；逆拓扑排序（每次删除出度为 0 的结点）：邻接表 $O(VE)$，邻接矩阵 $O(V^2)$，逆邻接表 $O(V+E)$ ；使用逆邻接表即可实现拓扑排序的正逆；使用 dfs 求拓扑序用DFS解拓扑排序
AOE 网（Activity On Edge NetWork），用 edge 表示活动，结点表示事件，只有一个入度为 0 的顶点（源点），一个出度为 0 的顶点（汇点）；源点到汇点的最长路径叫关键路径（可能有多条），上面的活动叫关键活动
事件的最早发生时间（ve，按照拓扑序求 max），活动的最早开始时间（e，弧起始点的 ve）
事件最迟发生时间（vl，按照逆拓扑序求 min），活动最迟开始时间（l）（ min（弧终点事件的最迟发生时间-活动时间））
活动的时间余量（d），活动的最早开始时间和最迟开始时间相同的活动（d=0）是关键活动

6.6 并查集¶

int fa[MAXN];

void init(int n) {
    for (int i = 0; i < n; i++) fa[i] = i;
}

int find(int x) {
    if (fa[x] != x) fa[x] = find(fa[x]);
    return fa[x];  
}

void unite(int x, int y) {
    int fx = find(a);
    int fy = find(b);
    fa[fx] = fy;
}

bool same(int x, int y) {
    return find(x) == find(y);
}

7 查找¶

7.1 基本概念¶

查找，查找表（数据集合），关键字（唯一标识数据的值）

静态查找表（只会查找），动态查找表（会进行插入和删除）,静态查找表用顺序存储，动态查找表用二叉排序树

平均查找长度 ASL

7.2 查找算法¶

顺序查找

哨兵（放在 a[0]，从尾部往前查找）
分析ASL，$ASL_{成功}=(n+1)/2,ASL_{失败}=n+1$
顺序查找的优化
有序表的顺序查找可以提前停止，用判定树分析，$ASL_{失败}=n/2+n/(n+1)$
被查找概率大的放在靠前的位置

折半查找

仅适用于有序的顺序表
查找效率分析 ASL，$O(long_2n)$
折半查找判定树的树高 $h=ceil(log_2(n+1))$ ，且是二叉排序树，且平衡，失败结点有 n+1

分块查找 / 索引顺序查找

块内无序，块间有序
先查索引表，可顺序，可二分（很麻烦）
查找效率分析，有 b 块，每块 s 个元素
顺序查找索引表，$ASL=\frac{b+1}{2}+\frac{s+1}{2}$，当 $s=\sqrt{n}$ 时，ASL 最小 = $\sqrt{n} + 1$
折半查找索引表，$ASL=ceil(log_2(b+1))+\frac{s+1}{2}$

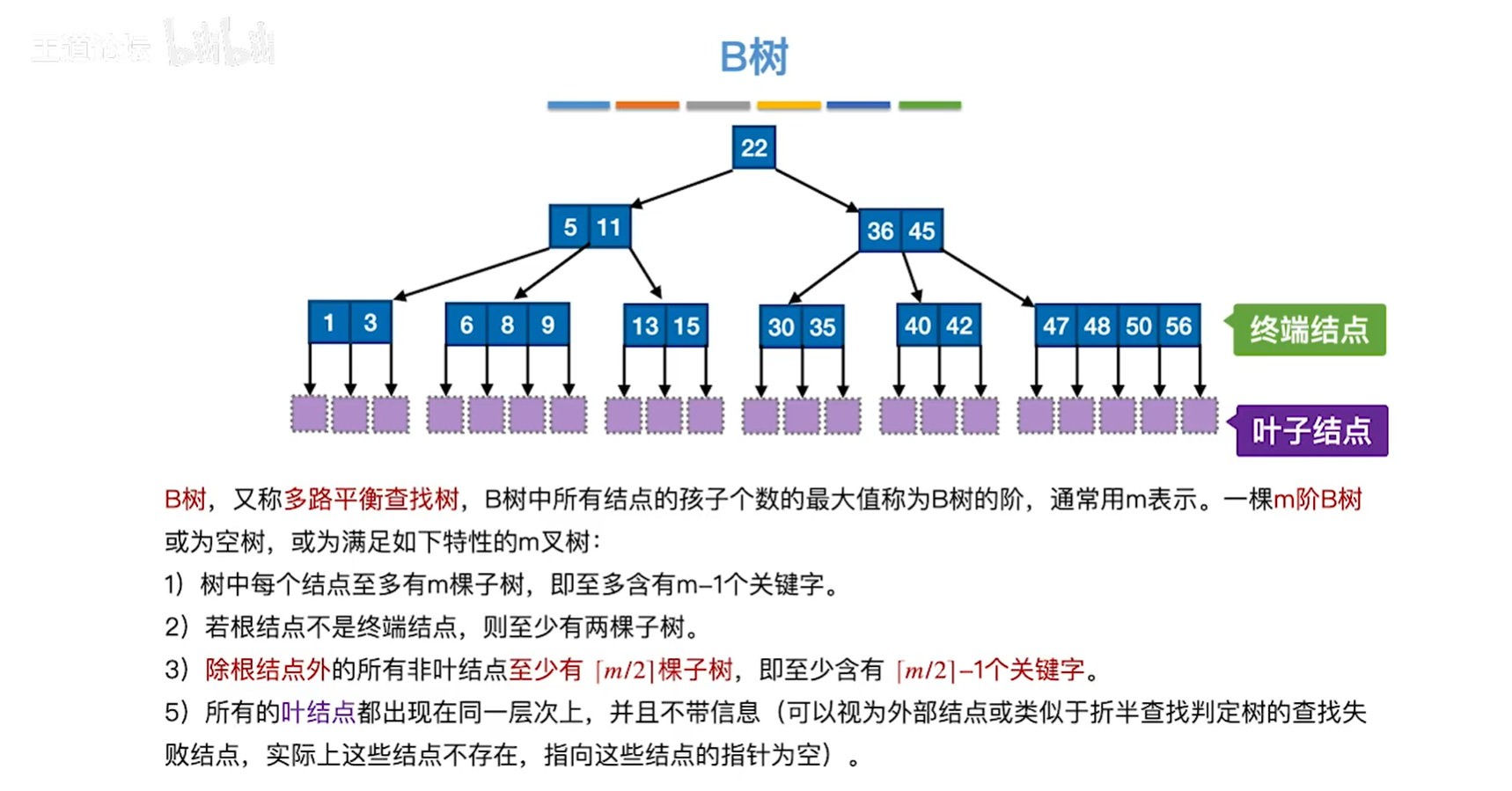
7.3 B树¶

二叉查找树变为 m 叉查找树，结点中的关键字是有序的，所以可以二分

struct Node {
    Elemtype keys[4]; // 最多4个关键字
    struct Node* child[5]; // 4个关键字最多5个分叉，最多5个孩子
    int num;    // 记录结点中有几个关键字
}

保证查找效率：

规定 m 叉查找树中除了根结点外，任何结点至少有 $ceil(m/2)$ 个分叉，$ceil(m/2)-1$ 个关键字
对于任何一个结点其子树的高度要相同

B树定义：

含 n 个关键字的 m 阶 B 树的最小高度： $$ n<=(m-1)(1+m+m^2+...+m^h) \ h >= log_m(n+1) $$ 最大高度：

思路一：

让各层分叉尽可能的小，第一层 2 个分叉，其他结点 $ceil(m/2)$ 分叉，所以各层结点数：$1,2,2ceil(m/2),...2ceil(m/2)^{h-2}$，则 $h+1$ 层共有叶子结点（失败结点）$2ceil(m/2)^{h-1}$ ；因为 n 个关键字的B树必有 n+1 个叶子结点（n个数字分成了 n+1 个区间），所以 $n+1>=2ceil(m/2)^{h-1}$，得 $h<=log_{ceil(m/2)}\frac{n+1}{2}+1$

思路二：设 $k=ceil(m/2)$

	最少结点数	最少关键字数
第一层	1	1
第二层	2	2(k-1)
第三层	2k	2k(k-1)
....	...	...
第h层	$2k^{h-2}$	$2k^{h-2}(k-1)$

h 层 m 阶 B 数至少包含关键字总数 $1+2(k-1)+...+2k^{h-2}(k-1)=1+2(k^{h-1}-1) <= n$，得 $h<=log_{ceil(m/2)}\frac{n+1}{2}+1$

B 树的插入（王道视频P73，书P297）：

如果只有根结点，就插入根结点，满了就分裂成 3 个结点（1个根结点 2 个子结点，根结点上传）
新元素一定要插入最底层的终端结点（保持失败结点在最底层的特性），满了也是分裂

B 树的删除（王道视频P73，书P298）：

要删除的关键字在终端结点，结点中关键字大于 $ceil(m/2)$ 就直接删除
如果不在终端结点中就直接用前驱或者直接后继（是在终端结点中的）代替，替代不影响关键字大于 $ceil(m/2)$ 的条件），如果小于了就让后继的后继（父节点下来，后继的后继当父节点）或者前驱的前驱（父节点下来，前驱的前驱当父节点）来填补，没的借就合并

B树插入删除

7.4 B+树¶

类比分块查找

定义2：非叶（形容词）根结点

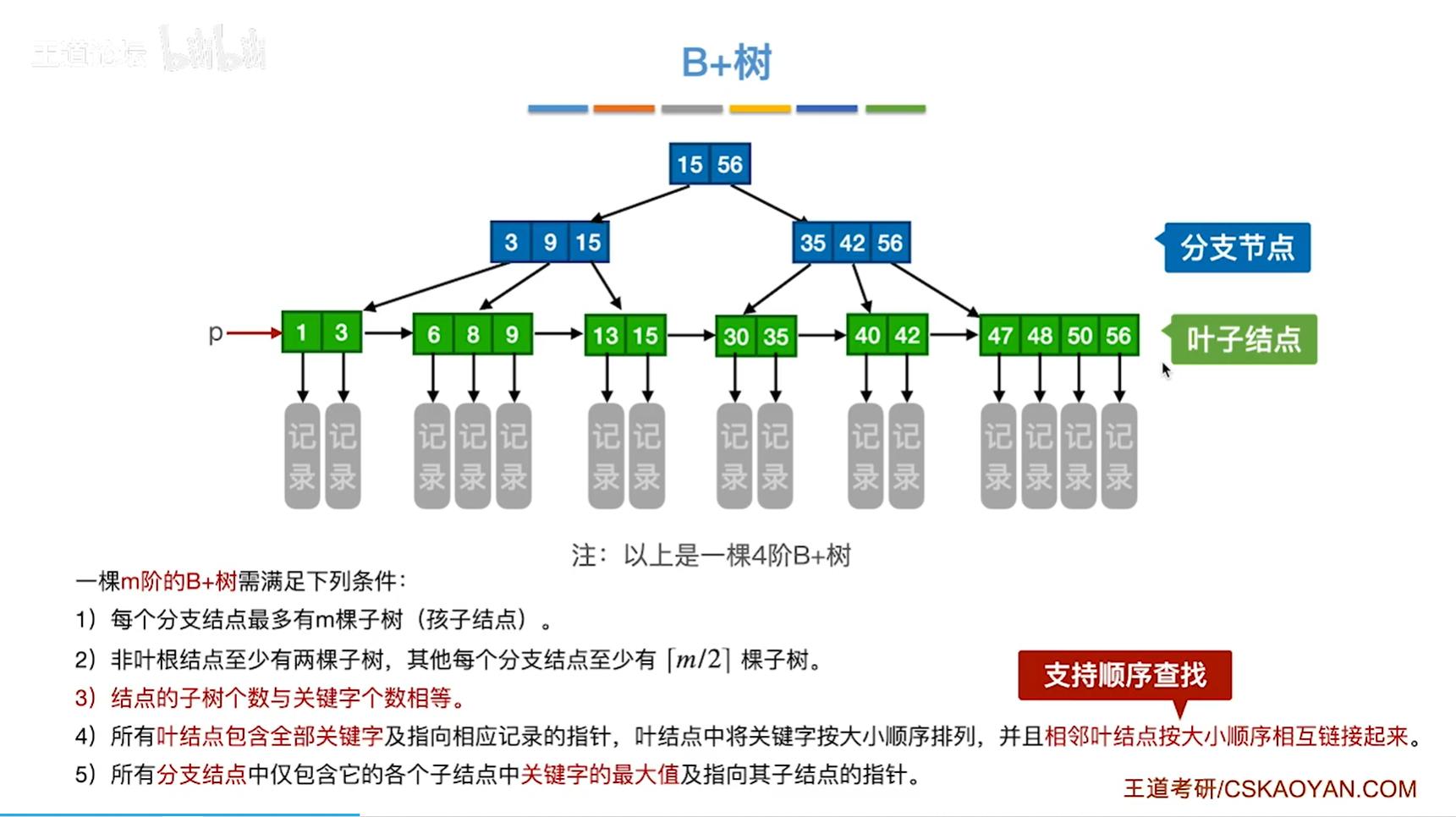
B+树的查找除了按照层次往下查找也可以按指针P顺序查找

B+树和B树的对比

m阶B+树：

结点中n个关键字对应n个子树
除根结点外的结点的关键字数 $[\ ceil(m/2),m\ ]$
叶子结点包含全部的关键字，非叶子结点中出现过的关键字也会在叶子结点中
所有非叶子结点只起到索引作用，不包含该关键字的对应记录的存储地址

m阶B树：

结点中n个关键字对应n+1个子树
除根结点外的结点的关键字数 $[\ ceil(m/2)-1, m-1\ ]$
各结点的关键字不重复
结点包含了关键字对应的记录的存储地址

7.5 散列查找¶

散列表=哈希表，散列函数=哈希函数，同义词，冲突，聚集

查找长度（如果是空，查找长度=0），计算 $ASL_{成功}$，$ASL_{失败}$（注意计算失败的时候主要和哈希函数有关和当前表内状态有关）

装填因子$\alpha$=表中记录数/散列表长度

常见散列函数：

除留余数法，散列表长度为 m，除数取不大于 m 的最大质数 p，会让哈希数值域小于散列表长度，再用开放定址法可以恢复
直接定址法，做一个线性变换 H(key) = a*key+b
数字分析法，选取数码分布均匀的若干位作为散列地址
平方取中法，取平方值的中间几位作为散列地址

处理冲突的方法：

拉链法，小优化：使链表有序，如果查找失败可以提前返回
开放定址法 $H_i=(H(key)+d_i)\%m$，查找失败时对空位置的判断也算一次比较；在删除结点时要做标记，以便后面查找时继续探测
线性探测法，$d_i=0,1,2,3,4...$
平方探测法（二次探测法），$d_i=0,1,-1,4,-4,9,-9...,k^2,-k^2$ ，$k<=m/2$，散列表长度 m 必须是一个可以表示成 4j+3 的素数才可以探测到所有素数
伪随机序列法
再散列法，多准备几个散列函数

注意在删除时要做标记，不然下次查找时可能会有问题

8 排序¶

这部分要注意代码

8.1 基本概念¶

空间和时间复杂度

算法的稳定性

分类：

内部排序，数据都在内存中，关注时间空间复杂度
外部排序，数据太多，无法全部放入内存，还要关注使读/写磁盘次数更少

8.2 插入排序：插入排序和希尔排序¶

插入排序：

每次将待排序的记录按照关键字大小插入前面已排好的子序列中
如果有哨兵，哨兵用来复制待排序的记录
空间复杂度 $O(1)$，时间复杂度 $O(n^2)$
稳定性：稳定
优化？：对前面已排好的子序列用折半查找，为了保证稳定性在找到之后还要继续找直到 low>high，然后把 [low, i-1] 内的元素右移，时间复杂度 $O(n^2)$
如果用链表存储，时间复杂度 $O(n^2)$

希尔排序：对插入排序的优化；由部分有序逼近全局有序

由增量 $d$ 分成多个子表后对子表插入排序，然后缩小增量 $d$ 直到 $d=1$；$d$ 建议初值为 $n/2$，然后每次 $d_{i+1}=d_i/2$；
空间复杂度：$O(1)$；时间复杂度： $O(n^{1.3}) 到 O(n^2)$
稳定性：不稳定
只能基于顺序表

8.3 交换排序：冒泡排序和快速排序¶

冒泡排序：

每轮都找到一个未排序的数放到最前面（或者找最大的放后面）
时间复杂度：$O(n^2)$ ，空间复杂度：$O(1)$
稳定性：稳定
冒泡排序适合链表
优化：某一趟没有交换就可以提前结束

快速排序（重要）：

在表中任取一个元素作为枢轴或基准，划分为左右 2 部分（实现时有一个 low 和 high 不断向内移动），然后递归
如果表原本就是有序或者逆序，时间复杂度：$O(n^2)$，空间复杂度：$O(n)$；如果基准元素选的好，时间复杂度：$O(nlog_2n)$，空间复杂度：$O(log_2n)$
枢轴的选取，选取头中尾三个元素选中间的，或者随机选择
稳定性：不稳定
一趟排序：可以确定多个元素的最终位置（比如第一趟确定1个，第二趟可以确定2个）；一次划分（partition）：只可以确定一个元素的最终位置

8.4 选择排序：简单选择排序和堆排序¶

选择排序：

在待排序的表中找到最小的，然后和待排序的表中第一个元素调换
空间复杂度：$O(1)$，时间复杂度：$(O(n^2))$，且无法提前停止，即在任何情况下时间复杂度不变；排序过程中移动次数很少
稳定性：不稳定
可以适用于链表

堆排序（重要）：

利用大根堆或小根堆实现；大根堆（大顶堆）：根结点的数大于左右子树
建立大根堆，检查非终端结点的编号 $i<=floor(n/2)$；编号从大到小检查，如果不比自己孩子结点都大，与 2 个孩子中大的交换，交换后还要向下检查（可能会破坏下面的堆的性质）；注意建立大根堆时表的下标一般从 1 开始方便计算孩子的下标
堆排序：每一趟将最后一个元素换到堆顶；再调整大根堆（小元素下坠）
时间复杂度：$O(nlog_2n)$，空间复杂度：$O(1)$
建立初始大根堆的复杂度：$O(n)$ ，不超过 4n
稳定性：不稳定

堆的插入和删除：以小根堆为例

插入：放在表尾（堆低），往上提
删除：用堆底（表尾）的元素替换删除的位置，然后向下坠；要注意下坠的时候如果有2个孩子，每次下坠都要对比2次，一个孩子只需要对比一次

8.5 归并排序和基数排序¶

归并排序：一般都是 2 路归并

将原序列拆成 2 部分进行递归归并排序
代码实现时有三个指针（int型），low，mid，high，开新的空间复制过去，在原列表中归并
2 个函数 MergeSort 和 Merge
时间复杂度：$O(nlog_2n)$，空间复杂度：$O(n)$ （merge中的辅助空间）
稳定性：稳定

基数排序：按个位先排好，再按十位排好。。。。

基数 $r$：比如十进制就是 10，表示有 10 种不同的取值
排序时需要设置 $r$ 个辅助队列，$Q_{r-1},...,Q_0$，按照权重低的到权重高的顺序，进行 $d$ 次分配再收集， $d$ 表示有几位
时间复杂度 $O(d(n+r))$，一趟分配 $O(n)$，一趟收集 $O(r)$，空间复杂度 $O(r)$，即 r 个辅助队列
稳定性：稳定
应用：按照学生年龄递减排序，权重年>月>日，年月日越大，年龄越小；所以第一躺按分配，收集按日递增，即先收集日小的。。。基数 $r$ 在年月日是不同的
基数排序擅长解决的问题：数据可以方便的拆分为 d 组，并且 d 和 r 小的

8.7 外部排序¶

外部排序：

外存和内存以块为单位读写
构造初始的归并段：在内存中开三块的空间，每次读入连续的 2 块进行归并排序，然后写回去，假设有 n 块，则得到 n/2 个归并段，一共读写了 2n 次；然后不断的归并成更大的段（这里要知道怎么用内存中三块的空间去归并，外存需要开额外的空间）
外部排序的时间开销=读写外存的时间+内部排序的时间（生成初始归并段）+内部归并所需时间；时间主要花在了读写外存上
总读写磁盘次数 = 文件总块数 *2* (归并趟数 + 1)（构造初始归并段+归并的趟数）
优化思路1：减少归并的趟数，可以使用多路归并，内存需要更多的缓冲区，空间换时间；假设有 r 个初始归并段，做 k 路归并

优化思路2：增加初始归并段的大小（内存需要的块数要变大），即减少初始归并段的数量 r

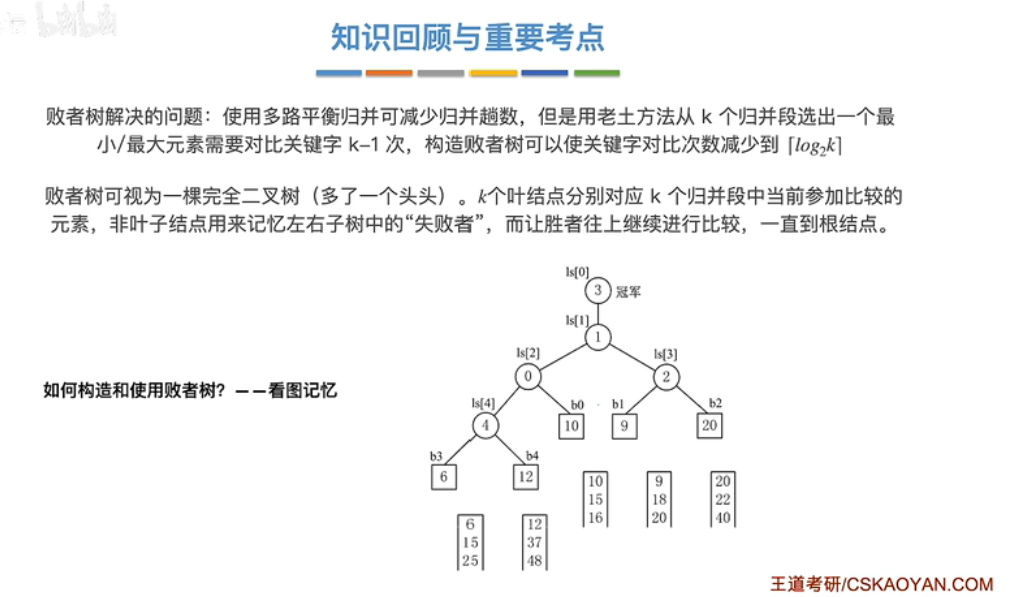
败者树：

k 路归并 k 过大时会导致选出一个最小元素需要对比 k-1 次，败者树可以优化这个；败者树的结点存放失败者，最后多一个额外的结点存储冠军

有了败者树，选出最小元素只需要对比关键字 $ceil(log_2k)$ 次

置换选择排序：

原本的办法，如果内存可容纳 $l$ 个记录，文件一共有 $n$ 个记录，则初始归并段的数量 $r = n/l$；

置换选择排序时记录已经输出的最小数值 $min$，每次输出最小的且大于 $min$ 的数，更新 $min$ 再读入新的；小于 $min$ 的留在内存内，直到内存内的都小于 $min$；这样做每次得到的初始归并段长度并不一定相同

最佳归并树

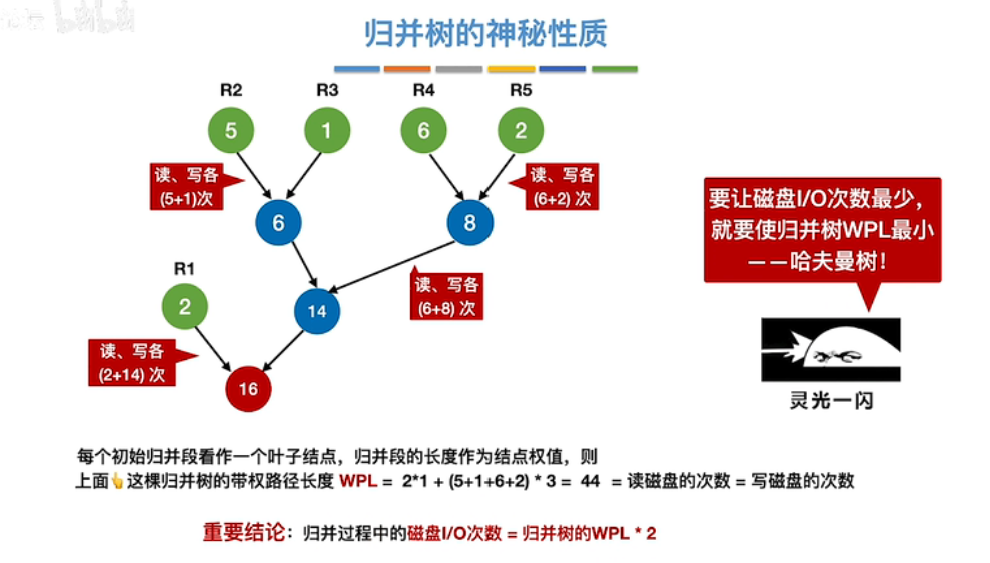
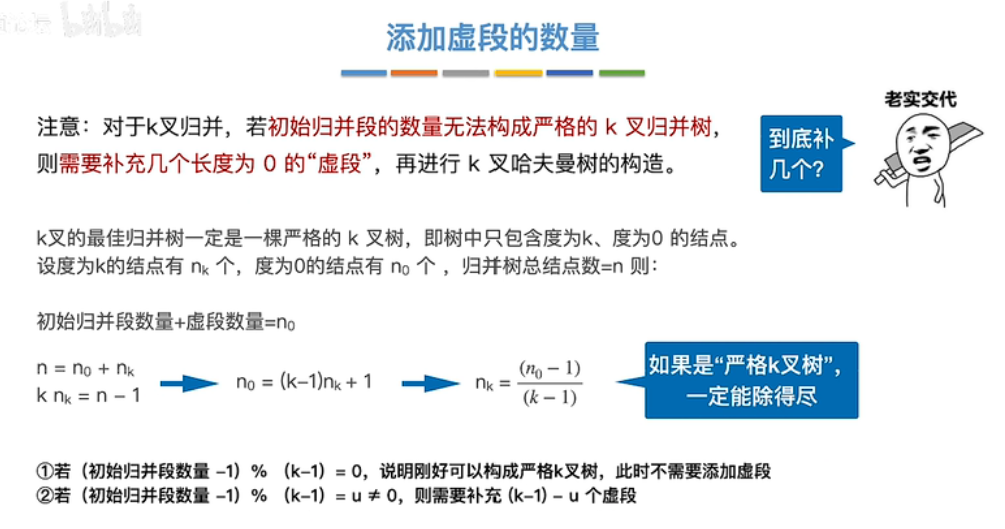
二路归并和多路归并原理相同，都是构造哈夫曼树；对于 k 叉归并，如果初始归并段数量无法严格构成 k 叉归并树，需要补充长度为 0 的 "虚段"

总结¶

串¶

next[i] 的值和模式串中 i 前的子串的最大相同前后缀长度 k 决定，如果串索引由1开始，就是 k+1，否则就是 k；
计算 next 的过程可以理解为模式串自己匹配自己的过程

树¶

哈夫曼树可以得到一种前缀编码，且带权路径长度是最小的（WPL）;且哈夫曼树无度为1的结点，$n_0=n_2+1$ 会很有用
并查集是一种简单的集合表示，find 如果不做路径压缩复杂度为 $O(n)$
二叉排序树和平衡二叉树
红黑树的定义，插入和删除

图¶

topological order：拓扑序，topological sequence：拓扑序列

基本概念

判断有向图是否有环：dfs，拓扑排序，求关键路径

查找¶

B 树和 B+ 树的区别（至多，至少）

B树中结点和关键字的区别

排序¶

直接插入排序比折半插入排序的比较次数多了
希尔排序的时间复杂度
堆排的初始化，插入，删除；要注意小元素下坠时要下坠多次
选择排序比较次数是固定的，归并排序比较次数的数量级是固定的
基数排序 LSD（最低位优先）的意思是先从最低为开始排，而不是最低位的重要性最大
外部排序常用归并排序

总的需要注意的点：

稳定的排序：插入，冒泡，归并，基数
每个算法的时间空间复杂度
最好情况下实践复杂度可以到达线性：冒泡排序，直接插入
排序有多个条件是，先比较重要性小的，再用稳定的排序算法比较重要性大的